Crypto
Practical Math
Practical Math

A protocol for exchanging public keys over an insecure channel.
Ab = (ga)b = (gb)a = Ba (mod p)
Computing 'a' given 'A' is very difficult when 'a' is large
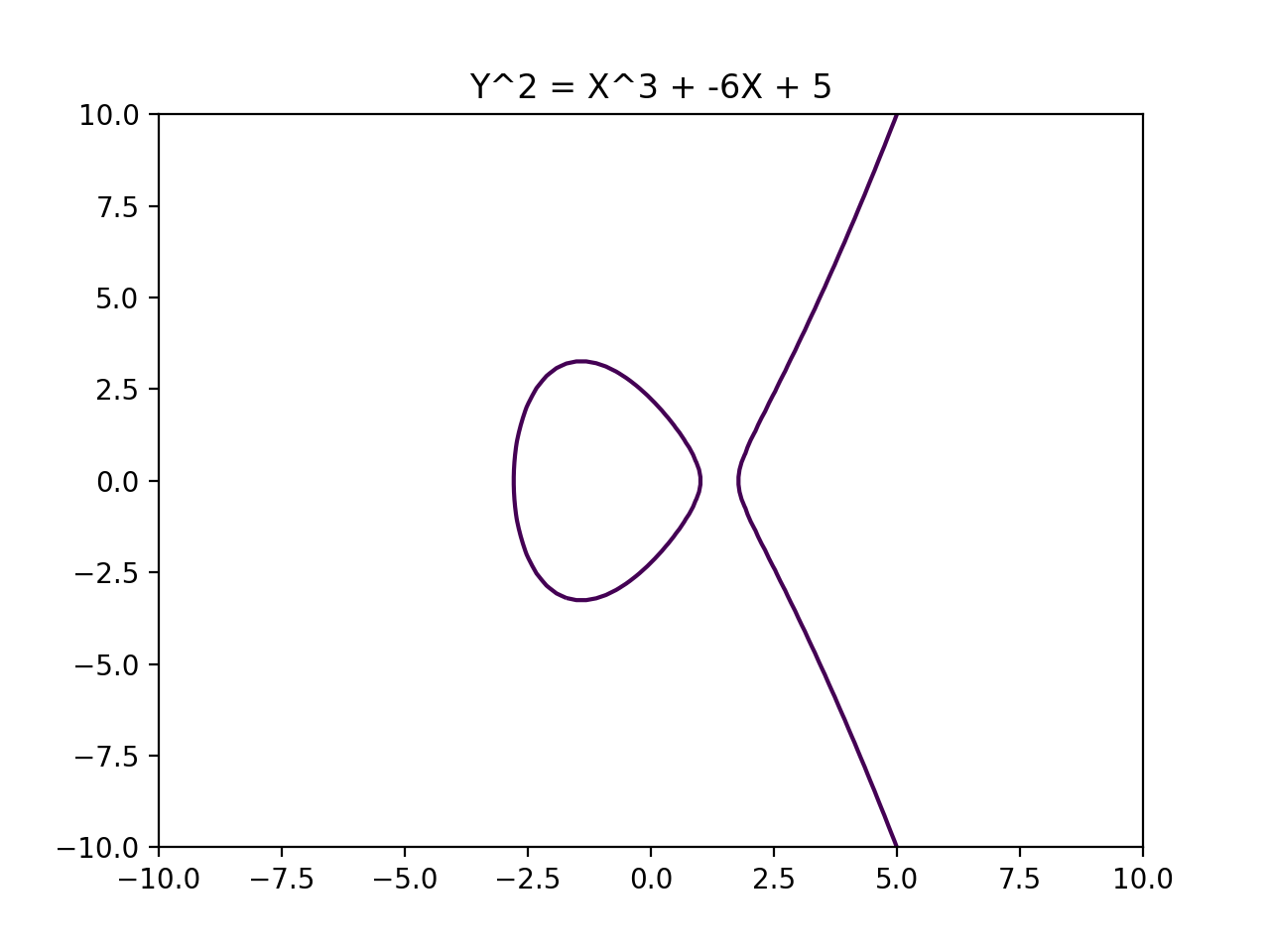
Public Key Cryptography which uses special properties of Elliptic Curves to create shared secrets.
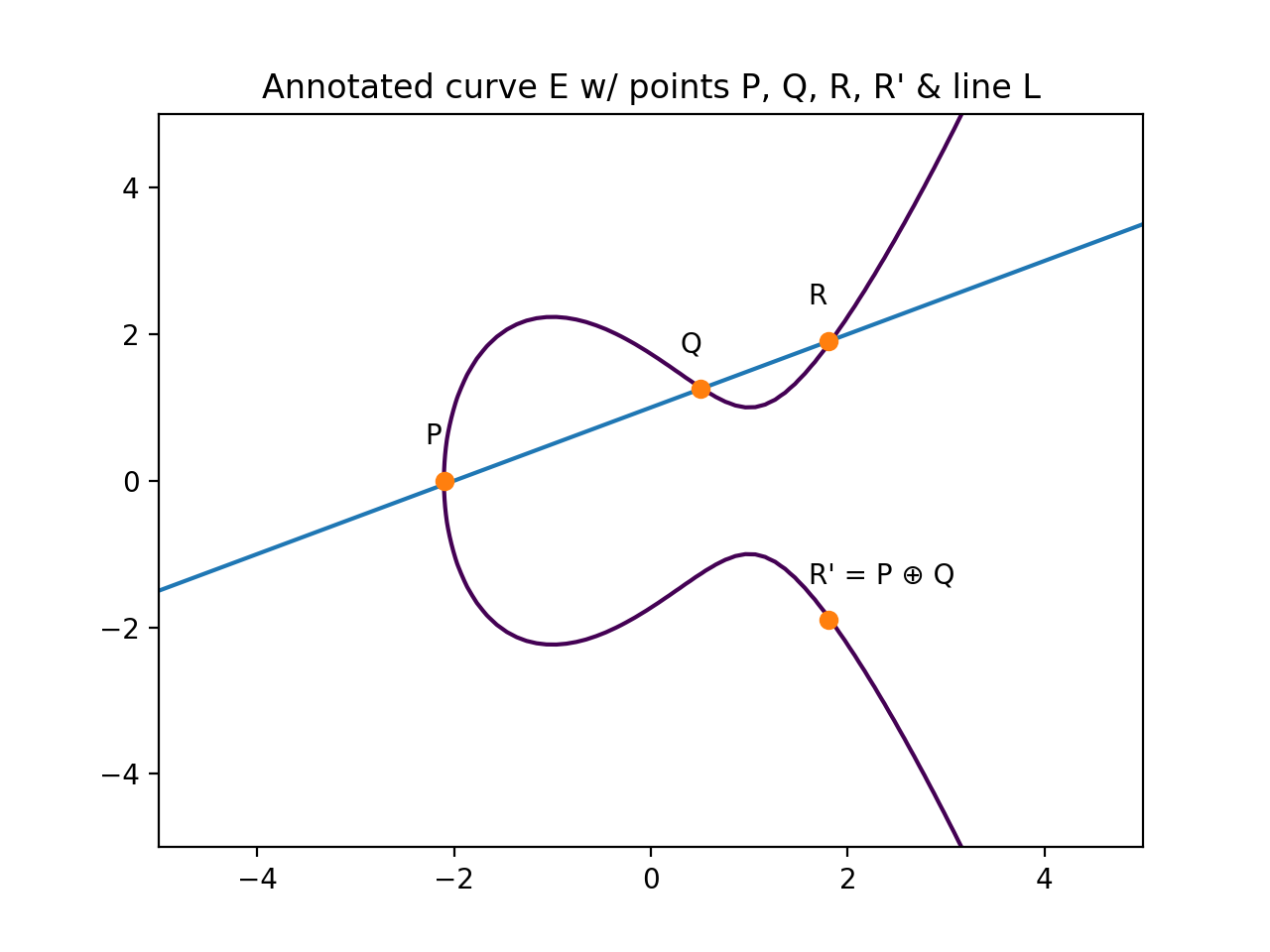
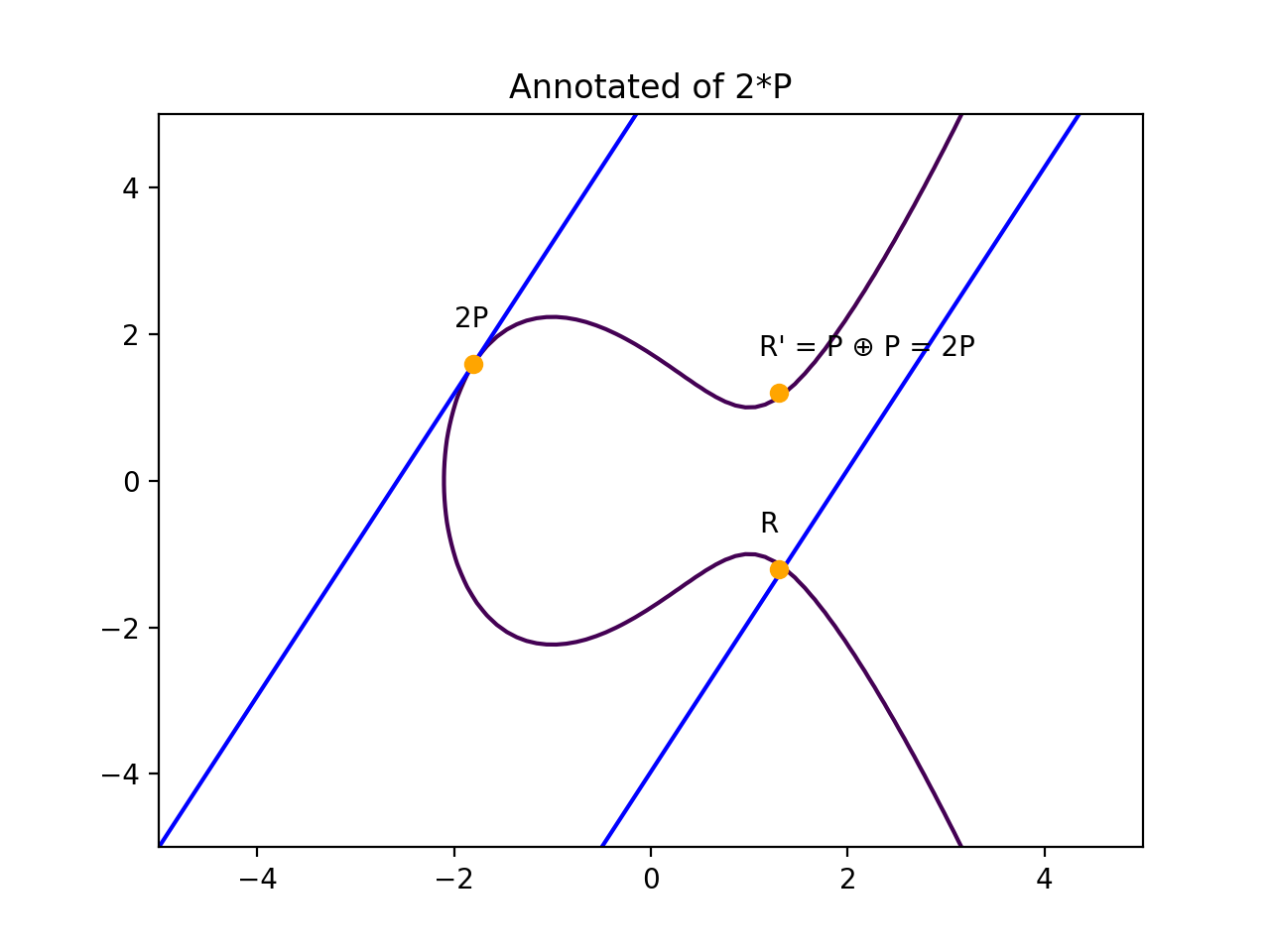
The "Double and Add" algorithm:
Greater security with less data.
[...] breaking a 228-bit RSA key requires less energy than boiling a teaspoon of water.
[...] breaking a 228-bit elliptic curve key requires enough energy to boil all the water on Earth.
Check your TLS Certs for _ECDHE_
Technical Details
Connection Encrypted (TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256, 128 bit keys, TLS 1.2)
A function that takes arbitrary size input and returns unique constant size output.
H("Mary had a little lamb"): 8774a25d2f
H("Pop"): 21129ffe98
H("Mary had a little lamb"): 8774a25d2f
H("password"): 6b3a55e026
H("123456"): e150a1ec81
H("hunter2"): 46a9d5bde7
...
H("qwerty"): 10231785cb
H(H(H(...H("SALTpassword")...))): c07e32d739
H(H(H(...H("SALT123456")...))): e0209a9bf0
H(H(H(...H("SALThunter2")...))): 3f02b38713
...
H(H(H(...H("SALTqwerty")...))): b2bb8650b7
Cryptographic Hash Functions:
| Algorithm | Secure? |
|---|---|
| MD5 | No |
| SHA-1 | No |
| SHA-256 | No-ish |
| SHA-512 | Yes-ish |
| SHA-3 | Yes |
Note
Fun Fact: The SHA family of hash functions were developed by the NSA!
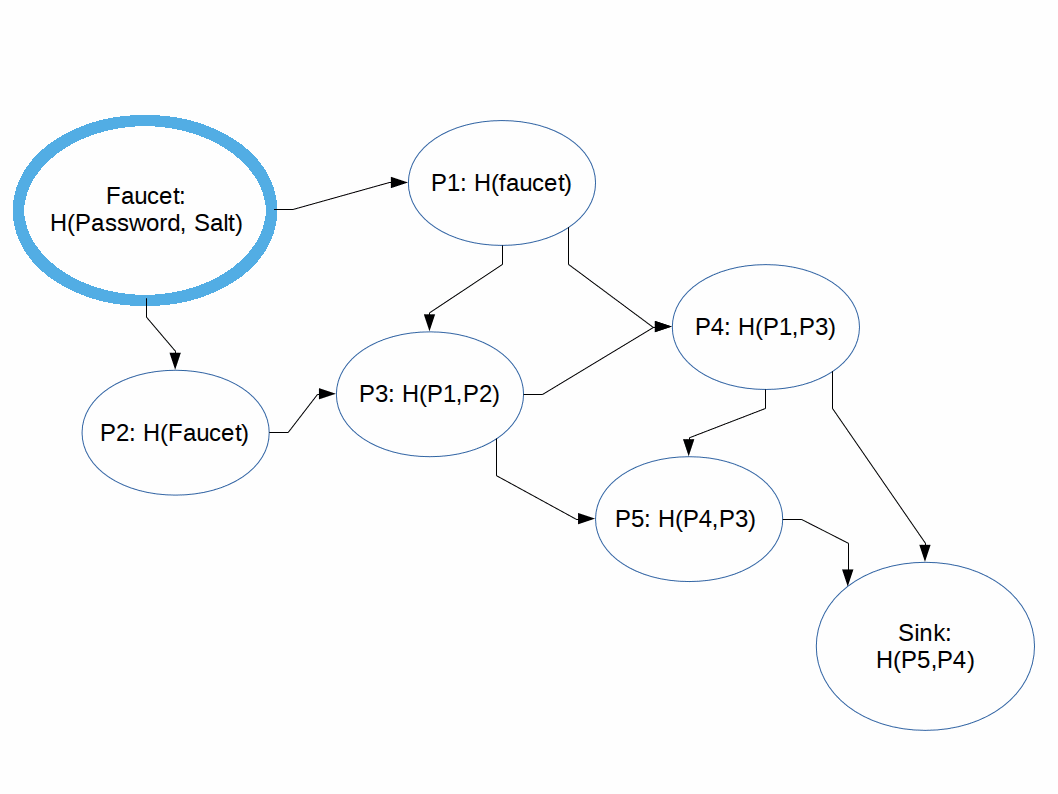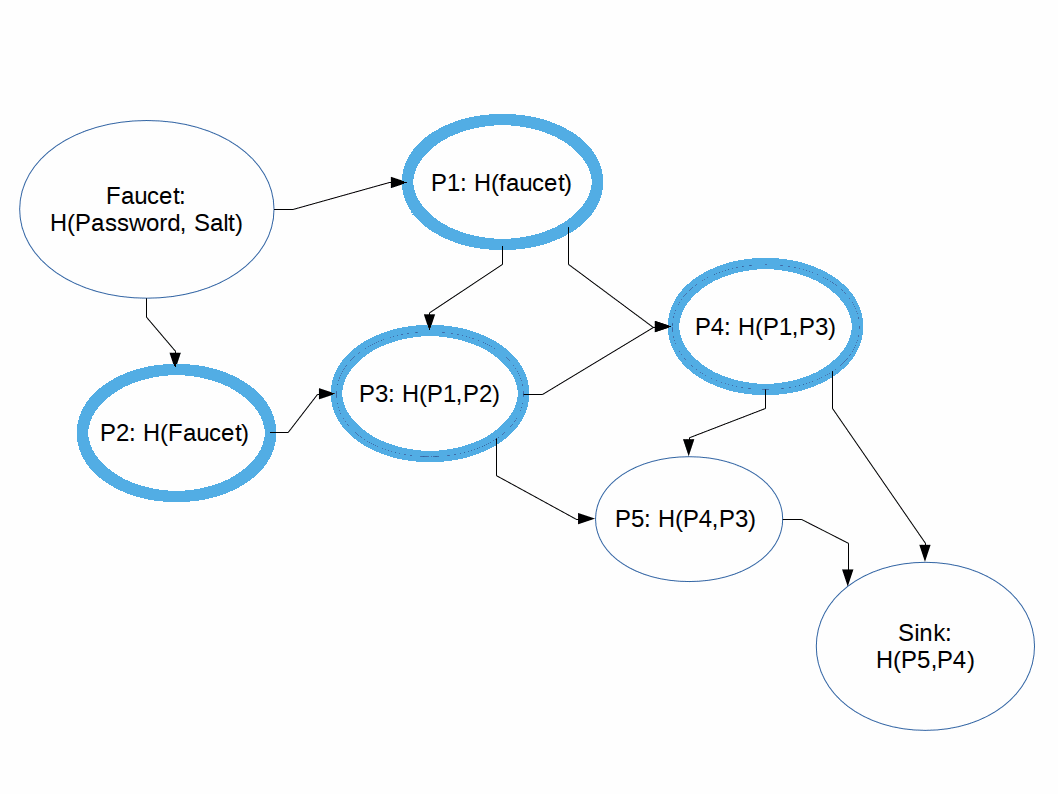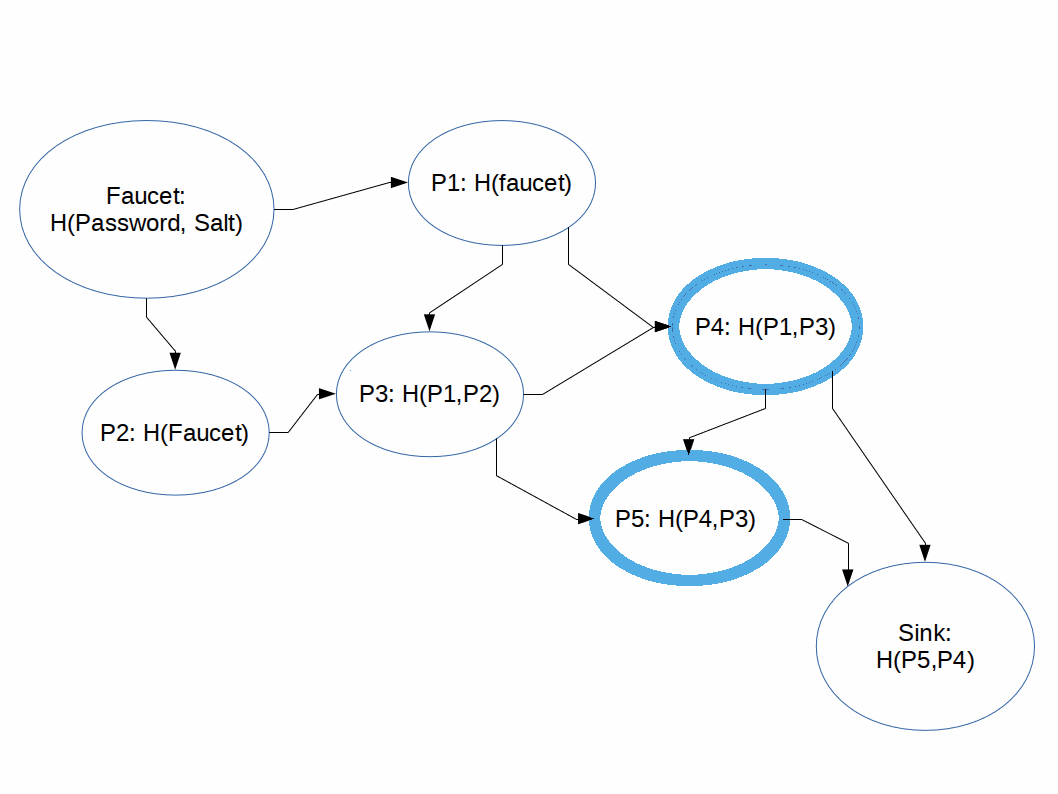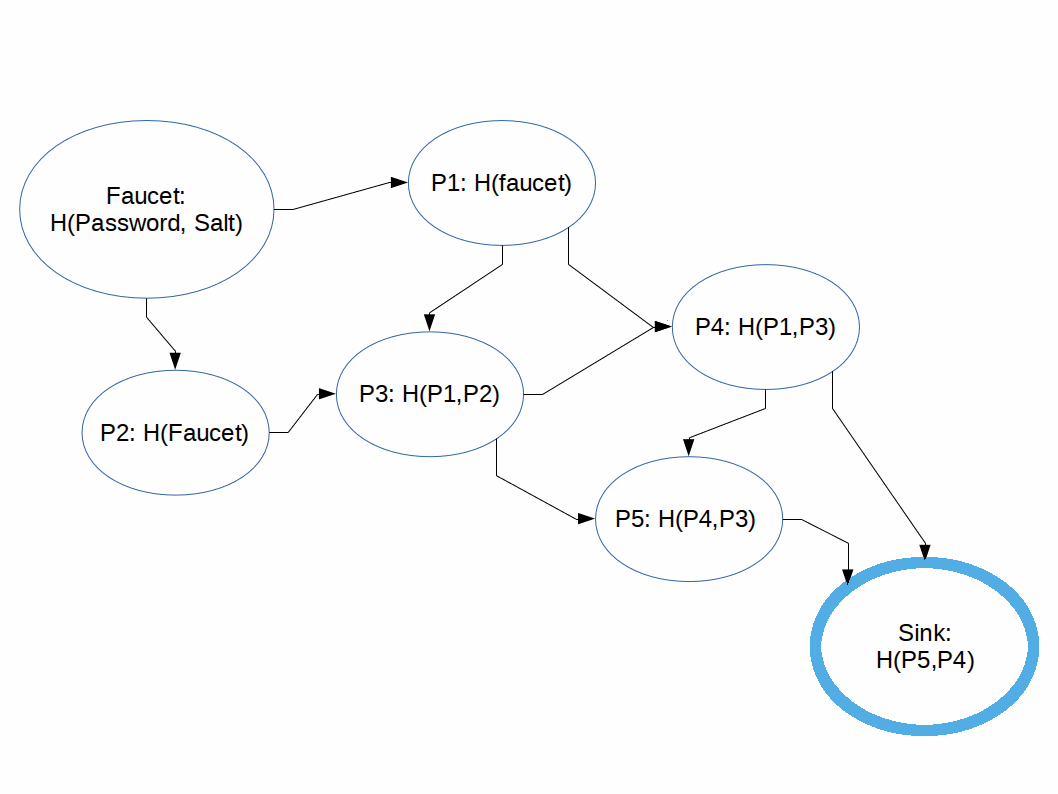
Hashing functions which are difficult to compute in memory-constrained systems.
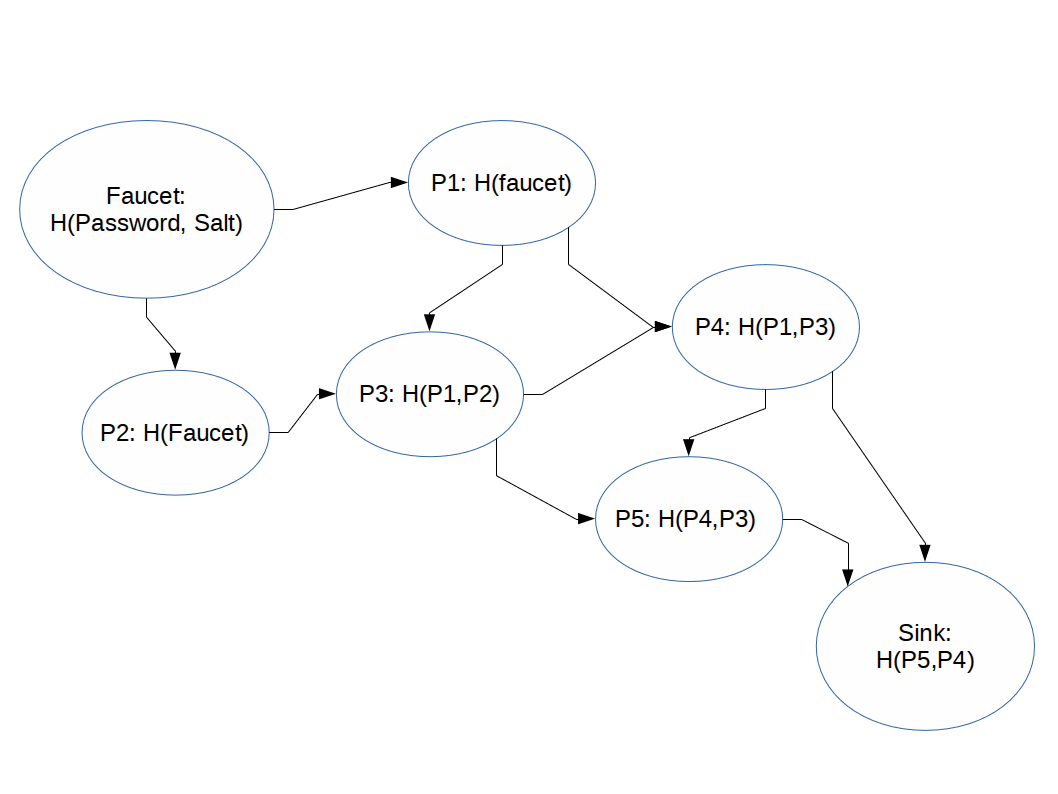

Before:
ASIC Hash Function Compute Time: 4 cycles (concurrent)
EC2 Hash Function Compute Time: 20 cycles
Memory Hard:
ASIC Memory Hard Hash Compute Time: 20+ cycles (sequential)
EC2 Memory Hard Hash Compute Time: 20 cycles
Scrypt
Evaluation of a program without knowledge of it's inputs or contents.
The Millionare Problem
function F = garbled(function f)
input A = obfuscated(input a)
input B = obfuscated(input b)
F(A,B) = f(a,b)
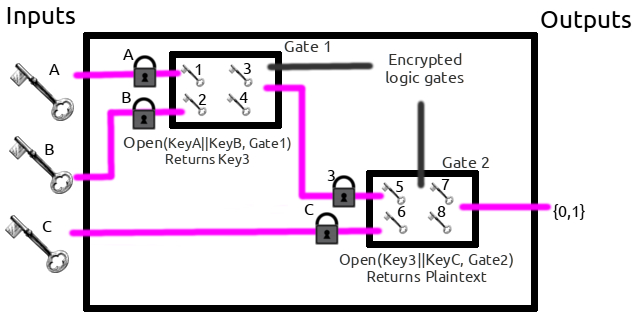
An implementation of secure multi-party calculations.
| OR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
1 or 0).Note
Now let's walk through an example where Alice and Bob will garble and evaluate an "OR" gate.
Kx0, Kx1, Ky0, and Ky1.Plaintext
| OR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Garbled
| OR | Kx0 |
Kx1 |
|---|---|---|
| Ky0 | B00 |
B01 |
| Ky1 | B10 |
B11 |
| OR | Kx0 | Kx1 |
|---|---|---|
| Ky0 | E( Kx0||Ky0, B00 ) |
E( Kx0||Ky1, B01 ) |
| Ky1 | E( Kx1||Ky0, B10 ) |
E( Kx1||Ky1, B11 ) |
Which looks like:
| OR | f4982f5cfd4 |
56198d52cb1 |
|---|---|---|
abfff1c5ed8 |
d9b2aefb1fe |
d56f56bb9bb |
abc7b0fb361 |
917df3320d7 |
4f2a86deb5e |
E( Kx0||ky0, B00), etc) and her input (KxA) to Bob.KxA.KyB.garbled_OR( KxA , KyB ) outputs 0 or 1.Note
Bob has enough information to get one of the four possible outputs of the circuit, but doesn't know if Alice's input is a 1 or a 0 at each circuit.
Importantly, while Bob can share the output of the circuit, he should not share his input. That would make using OT (step 6) obtuse.
Contact sharing.
Note
Good question.

Note
This matters for a few reasons:
THESIS THESIS THESIS???